گنجینه دانستنی ها و معماهای هوش و ریاضی

همچنین تمامی شبکه های اجتماعی رسمی آی هوش، در خود وب سایت معرفی شده است و خواهشمند است به سایر رسانه هایی که خودشان را به آی هوش منتسب می نمایند، توجه نفرمایید.

با سپاس

مدیریت آی هوش

وبلاگ آی هوش آی هوش

آی هوش جمعه 5 آذر 1395 ساعت 11:56

0 نظر

تدریس ریاضی و هوش های چندگانه (قسمت دوم)

یک برنامه درسی موفق، برنامه ای است که بتواند برای تمام سبک های یادگیری مختلف، راهکارهایی برای یادگیری ارائه کند. کلاس ریاضی نیز بی شک می تواند از تکنیک های آموزش منطبق با هوش های چندگانه بهره مند شود. معلمین ریاضی می توانند از طریق توجه به سبک های یادگیری و هوش های مختلف دانش آموزان، کلاس ریاضی را برای همه به یکسان جذاب و قابل درک کنند. در مقاله قبلی به تاثیر هوش کلامی، موسیقایی و هوش حرکتی بر آموزش ریاضی پرداختیم در ادامه نیز استفاده از سایر انواع هوش را در آموزش و یادگیری ریاضی مورد بررسی قرار می دهیم.

هوش فضایی- دیداری و آموزش ریاضی:
دانش آموزان دارای هوش فضایی – دیداری بالا، نگاه تیزبین و دقیقی دارند. آنها بر قدرت بینایی خود برای یادگیری متکی هستند و از طریق دیدن می آموزند بنابراین، برای به کار گیری قدرت دیداری و تجسم فضایی این دانش آموزان در تدریس ریاضی از این روش های استفاده کنید:

- مراقب باشید که وقت کلاس را تنها به سخنرانی نگذرانید. هنگام توضیح دادن درس، مرتب از تصاویر و رسم اشکال و نمودارها روی تخته سیاه استفاده کنید.

- از اشکال، نمودارها، جداول و احجام برای توضیح مفاهیم درس استفاده کنید و دانش آموزان را برای استفاده از آنها تشویق کنید. از آنها بخواهید مفاهیم درس را روی دفترشان طراحی کنند، نمودار رسم کنند، شکل بکشند حتی می توانند از اشکال یا طرح های کمیک و طنز برای یادسپاری مفاهیم درسی در حاشیه کتاب ها یا دفاتر ریاضی خود استفاده کنند.

- برای توضیح مفاهیم ریاضی و به خصوص هندسه از محیط پیرامونی مثال بزنید. برای نمونه درس کسر را با تجسم یک پیتزا و تقسیم آن ارتباط دهید. از شکل کندوی زنبور عسل برای توضیح شش ضلعی ها استفاده کنید. به کودکان کمک کنید، درس را در محیط زندگی واقعی خود تجربه کنند و نمادهای مهم را به خاطر سپارند.

هوش منطقی و آموزش ریاضی:
شاید بیشترین ارتباط بین هوش های گاردنر و موفقیت ریاضی، وابسته به هوش ریاضی- منطقی باشد اما برای به کارگیری این هوش نیز باید به دانش آموزان کمک کرد. افراد دارای هوش ریاضی- منطقی بالا، به سادگی می توانند روابط بین عناصر مختلف را کشف کنند، در طبقه بندی و مجموعه سازی موفق هستند. این افراد، قدرت زیادی در درک روابط عددی و نظم و منطق دارند بنابراین در کلاس ریاضی، برای کمک به دانش آموزان دارای هوش منطقی بالا از این روشها استفاده کنید:

- به کارگیری محاسبات ذهنی را تشویق کنید. بگذارید این دانش آموزان از ذهن خود برای انجام عملیات ریاضی و حل مسائل استفاده کنند. این افراد در استفاده از محاسبات ذهنی، سرعت بالاتری نسبت به استفاده از وسایل کمک آموزشی دارند.

- از این دانش آموزان بخواهید قبل از حل مسئله، نتیجه آن را حدس بزنند. این روش به آنها کمک می کند با استفاده از محاسبات ذهنی، روابط بین اعداد و معادلات را کشف کنند.

- موقع تدریس هر مبحث، آن را با سایر مباحث ریاضی نیز مرتبط کنید. برای مثال وقتی کسر یک دوازدهم را می آموزید، به موضوع ساعت، خواص دایره و همین طور درجات (360 درجه) اشاره کنید. این دانش آموزان از برقراری روابط منطقی بین مباحث و مفاهیم مختلف لذت می برند و یادگیری عمیق تری کسب می کنند.

هوش اجتماعی و آموزش ریاضی:
شاید فکر کنید هیچ ارتباطی بین هوش اجتماعی و یادگیری ریاضی وجود ندارد ولی در اشتباه هستید حتی می توان از هوش اجتماعی نیز در تدریس ریاضی استفاده کرد. افرادی که هوش اجتماعی بالایی دارند، از مصاحبت و دوستی با دیگران لذت می برند این افراد کارهای گروهی و با هم بودن را دوست دارند و در کنار دیگران می آموزند. بنابراین در کلاس ریاضی از این راهکارها استفاده کنید:

- کلاس را به چند گروه تقسیم کنید و این افراد را در گروه های دو یا چند نفره قرار دهید. به هر گروه، تکالیف و تمرینات مختلفی بدهید و بخواهید به کمک یکدیگر مباحث درس را تمرین کنند.

- بیوگرافی بزرگان ریاضی را در کلاس تعریف کنید و در مورد زندگی و فعالیت های آنان داستان های جالبی تعریف کنید. برای مثال وقتی قانون فیثاغورث را درس می دهید، گریزی هم به زندگی او بزنید. شرح حال این بزرگان به کودکان انگیزه می دهد و احساس همزادپنداری را در آن تقویت می کند چرا که هوش اجتماعی بالا با احساس همدلی و درک دیگران رابطه مستقیمی دارد.

- به این دانش آموزان فرصت دهید حتی بعد از ساعت کلاس نیز با شما در ارتباط باشد و سوالات خود را از شما بپرسد. البته این دانش آموزان به سبب هوش اجتماعی بالای خود، به طور ذاتی محبوب و دوست داشتنی هستند و بعید است شما بتوانید درخواست آنها را برای پاسخ به سوالاتشان و راهنمایی خارج از کلاس رد کنید.

هوش درون فردی و آموزش ریاضی:
دانش آموزانی که هوش درون فردی بالا دارند، درک عمیقی از روحیات، احساسات و ارزش های درونی خود دارند. آنها معمولا برای یادگیری به خلوت و تنهایی نیاز دارند. برای آموزش ریاضی به دانش آموزانی با هوش درون فردی بالا از این روشها استفاده کنید:

- با این دانش آموزان به طور اختصاصی صحبت کنید و از آنها بخواهید به شما توضیح دهند که چگونه به ریاضی نگاه می کنند. چه احساس و چه نگرانی هایی دارند. بگذارید پروسه تفکر خود و راه حل مسائل را برای شما توضیح دهند.

- به این دانش آموزان فرصت دهید، روش خاص خود را برای حل مسئله بیابند. ریاضی را به روش خود حل کنند و با آن ارتباط بگیرند.

- از احساسات و افکار خود در حل مسائل برای آنها مثال بزنید مثلا بگوئید که وقتی یک مسئله را حل می کنید چه راههایی را امتحان می کنید چه احساساتی دارید و برای پیدا کردن پاسخ، چه تلاشی می کنید.

- به این کودکان فرصت دهید به تنهایی و با تمرکز بالا مشغول حل تمرینات شوند، آنها را به اجبار وادار به شرکت در گروه ها نکنید اجازه بدهید در خلوت خود به حل مسائل فکر کنند.

منبع: تدریس ریاضی و هوش های چندگانه (قسمت دوم)

:: اختصاصی گروه تدوین محتوای آی هوش

استفاده از این مطلب و انتشار آن، با ذکر نام آی هوش و درج لینک www.ihoosh.ir، بلا مانع است.

اختصاصی آی هوش هوش هوش چندگانه

آی هوش دوشنبه 17 شهریور 1393 ساعت 11:24

0 نظر

تدریس ریاضی و هوش های چندگانه (قسمت اول)

کلاس درس ریاضی برای بسیاری از دانش آموزان به خودی خود استرس زا است اما جالب است که بدانیم بخش کمی از این مشکل مستقیما به خود درس ریاضی باز می گردد. تحقیقات زیادی در سراسر دنیا نشان می دهند که آنچه موجب نگرانی و یا دلسردی دانش آموزان از موفقیت در ریاضی می شود، بیش از آنکه مربوط به مباحث آن باشد، به روش تدریس ریاضی وابسته است. معمولا معلم های ریاضی، روش واحدی را برای تدریس آن به کار می برند، درس را توضیح می دهند پای تخته چند مسئله حل می کنند و سرانجام چند تمرین کلاسی و تکلیف منزل به بچه ها می دهند و این تمام کاری است که در اکثر کلاس های ریاضی انجام می شود. اما آیا به راستی این روش تدریس در یادگیری دانش آموزان موثر است؟

هاوارد گاردنر، در سال 1983، بحث مهمی را وارد روان شناسی یادگیری نمود مبحثی که او گشوده بود به تئوری هوش های چندگانه مشهور شد. او براین باور بود که هوش، مفهومی مستقل و یکپارچه نیست بلکه انسان ها هوش های مختلفی دارند و هر یک در برخی از جنبه های مختلف هوش، نقاط قوت و ضعف دارند. او در تئوری خود هشت نوع هوش مختلف را معرفی کرد: هوش کلامی، هوش ریاضی- منطقی، هوش بدنی-حرکتی، هوش فضایی-دیداری، هوش طبیعی، هوش موسیقایی، هوش اجتماعی، هوش درون فردی. که البته بعدها یک نوع دیگر هوش را هم به تئوری خود اضافه نمود که از آن به عنوان هوش وجودی نام برد.

کاربرد تئوری هوش های چندگانه گاردنر بیش از هر جای دیگر در روان شناسی آموزشی خود را نشان داد. آموزشگران زیادی در سراسر جهان سعی در تطبیق روشهای تدریس خود در کلاس های درس بر اساس تئوری هوش های چندگانه کردند و موفقیت های چشمگیری نیز به دست آوردند. این تئوری مدعی است که انسان ها به روش های مختلفی می آموزند و روش یادگیری آنها منطبق بر انواع هوش های آنهاست. به عبارت دیگر بسته به اینکه هر کس در کدام یک از انواع هوش، قوی و مستعد باشد، روش یادگیری او نیز منطبق با نیازها و خصائص آن هوش طبقه بندی می شود. برای مثال فردی که هوش موسیقایی بالایی دارد، از طریق شنیدن اصوات و آهنگ ها می تواند بیاموزد کسی که هوش کلامی بالایی دارد از راه سخن گفتن، نوشتن و ارتباطات کلامی، یاد می گیرد و به همین ترتیب سایر انواع هوش نیز بر روش یادگیری انسان ها تاثیر می گذارد. به نظر گاردنر کلاس درس موفق، کلاسی است که از همه انواع هوش برای تدریس مواد آموزشی استفاده شود تا بیشترین بازده و بیشترین یادگیری توسط دانش آموزان به دست آید.

بی شک تدریس ریاضی نیز نمی تواند از این قاعده مستثنا باشد. روش های یادگیری مختلف منطبق با هوش های چندگانه در تدریس و یادگیری ریاضی نیز موثر است در این مقاله به تفکیک بر روش هایی متمرکز می شویم که از طریق به کارگیری هوش های چندگانه به تدریس مباحاث ریاضی کمک می شود:

هوش موسیقایی و آموزش ریاضی:
افرادی که دارای هوش موسیقایی بالا هستند، از طریق گوش دادن به اصوات و آهنگ ها می آموزند. این افراد به راحتی قادرند ضرباهنگ را تشخیص دهند، ریتم را پی بگیرند و به طور کلی ذهن آهنگین و موزونی دارند. از این نظر در کلاس درس نیز از طریق گوش دادن، تشخیص تم و لحن می آموزند. برای کمک به این افراد در یادگیری ریاضی می توان از این طرق عمل کرد:

- هر جا که می توانید از آهنگ ها و موسیقی استفاده کنید. برای مثال جدول ضرب را با یک ریتم آهنگین بخوانید و دانش آموزان را تشویق کنید آن را به طور آهنگین به ذهن بسپارند.

- به دانش آموزان اجازه بدهید اگر دوست دارند هنگام حل مسئله و تمرکز بر مباحث ریاضی از یک موسیقی پس زمینه استفاده کنند. موسیقی به آنها آرامش می دهد و کمک می کند بیشتر روی مباحث درسی متمرکز شوند.

- دانش آموزان را تشویق کنید نواختن یک ساز را آغاز کنند و موسیقی بیاموزند. تحقیقات زیادی، رابطه بین یادگیری موسیقی و ریاضی را به اثبات رسانده اند. موسیقی سراسر خلاقیت در قالبی منظم و ریتمیک است و یک آهنگ را هم از نظر اصوات و هم نظم هجایی می توان به زبان ریاضی ترجمه کرد. یادگیری موسیقی به طور غیر مستقیم به درک مفاهیم ریاضی کمک شایانی می کند.

هوش کلامی و آموزش ریاضی:
این دانش آموزان از طریق صحبت کردن، نوشتن و خواندن می آموزند بنابراین باید سعی کنید ارتباطی را بین زبان و ریاضی برقرار کنید:

- درس را توضیح دهید. مراحل حل مسئله و حتی نوع دیدگاه خود را به مباحث ریاضی مطرح کنید در مورد روش حل مسئله در کلاس بحث کنید و از دانش آموزان نیز بخواهید شیوه حل مسئله را به زبان خود شرح دهند. توضیح مباحث ریاضی به درک عمیق دانش آموزان با هوش کلامی بالا کمک می کند.

- منابع مطالعاتی به دانش آموزان با هوش کلامی بالا کمک می کند که از طریق خواندن، بیاموزند. کتاب های درسی و کمک درسی که حاوی توضیحات در مورد مفاهیم و روش های حل مسئله هستند به این دانش آموزان کمک می کنند با فراغ بال و آرامش کافی در وقت آزاد خود به مطالعه و تعمق در مباحث ریاضی بپردازند. به دانش آموزان خود چند منبع مطالعاتی نظیر کتاب، جزوه درسی، و سایت های اینترنتی آموزشی معرفی کنید.

- سعی کنید کلمات و اصطلاحات علمی رایج در ریاضی را برای دانش آموزان موشکافی کنید و ریشه کلمات را بیابید. برای مثال وقتی به مبحث مثلث ها می رسید توضیح بدهید مثلث یعنی چه، یا اینکه مثلث متساوی الاضلاع، یا متساوی الساقین، چه معنای لغوی دارد. وقتی دانش آموزان با ریشه یک لغت یا اصطلاح ریاضی آشنا می شوند، درک عمیق تری نسبت به خصوصیات آن در علم ریاضی و هندسه نیز کسب می کنند.

هوش بدنی- حرکتی و آموزش ریاضی:
دانش آموزانی که هوش حرکتی بالایی دارند، عاشق جست و خیز و حرکت هستند این افراد از ساکن نشستن و گوش دادن به سخنرانی های طولانی خسته می شوند. آنها نیاز دارند هنگام یادگیری قسمتی از بدن خود را حرکت دهند. بنابراین:

- به این دانش آموزان اجازه بدهید آزادانه در کلاس حرکت کنند اگر لازم است جلوی تخته بیایند یا به میز همکلاسی های خود سرکشی کنند. اجازه بدهید اگر دوست دارند وقتی شما مشغول تدریس ریاضی هستید، بایستند یا کمی در جای خود جا به جا شوند. حرکت به جای اینکه سبب حواسپرتی آنها شود، به آنان تمرکز بیشتری می بخشد.

- به این دانش آموزان کمک کنید برای درک مباحث ریاضی از بدن خود استفاده کنند. حرکت دست ها وانگشتان و یا حتی قسمت هایی از بدن می تواند به آنها کمک کند بین مفاهیم ریاضی و بدن خود ارتباط ایجاد کنند. استفاده از انگشتان برای شمردن در سالهای اول ابتدایی به این دانش آموزان کمک زیادی می کند. استفاده از ابزار، و وسایل کمک آموزشی که قادر به جا به جا کردن آنها باشند، به این کودکان امکان درک عمیق از ریاضی را می دهد.

- مباحث ریاضی را با حرکت و جنبش مخلوط کنید. اگر درس اشکال هندسی را می دهید با گچ روی زمین، مثلث یا مربع بکشید و از این دانش آموزان بخواهید روی راس های آن بایستند یا از روی اضلاع حرکت کنند. کارهای دستی مثل ساختن احجام هندسی و حرکت در فضای کلاس به درک مباحث ریاضی کمک می کند.

منبع: تدریس ریاضی و هوش های چندگانه (قسمت اول)

:: اختصاصی گروه تدوین محتوای آی هوش

استفاده از این مطلب و انتشار آن، با ذکر نام آی هوش و درج لینک www.ihoosh.ir، بلا مانع است.

هوش اختصاصی آی هوش هوش چندگانه آموزش ریاضی

آی هوش دوشنبه 17 شهریور 1393 ساعت 11:13

0 نظر

مریم میرزاخانی

مریم میرزاخانی

آی هوش جمعه 31 مرداد 1393 ساعت 16:54

0 نظر

رویا بهشتی زواره

نام: رویا بهشتی زواره (Roya Beheshti Zavareh)

تولد: 1977 - اصفهان - ایران
ملیت: ایرانی
دکترای دانشگاه ام آی تی، ورودی ۱۳۷۴ ریاضی دانشگاه صنعتی شریف
شهرت: ریاضیات، هندسه جبری
نشانی صفحه رسمی: http://www.math.wustl.edu/~beheshti

رویا بهشتی زواره، متولد 1356 در اصفهان است. رؤیا، در المپیاد سال 1994 هنگ کنگ در حالیکه فقط 17 سال داشت، همراه با دیگر همراهانش افتخار آفریدند. او موفق شد در این دوره، مدال برنز را کسب نماید. اسامی دانش آموزان تیم ایران در سی و پنجمین المپیاد جهانی ریاضی به شرح زیر بود:

مازیار رامین راد، مریم میرزاخانی (مدال طلا)، رضا صادقی، رویا بهشتی زواره (مدال نقره)، علی نور محمدی و امید نقشینن (مدال برنز)

$کسب مدال نقره المپیاد ریاضی 1994 توسط رویا بهشتی زواره$

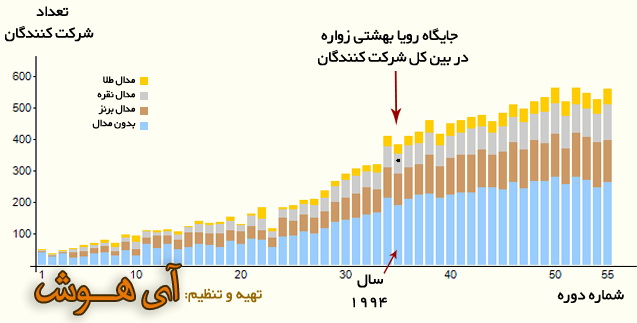
«مریم» و «رؤیا» از زبان مدیر دبیرستان فرزانگان:

خیریه‌بیگم حائری‌زاده، مدیر پیشین مجتمع آموزشی فرزانگان در مورد او و دست صمیمی اش مریم میرزاخانی چنین می گوید:

"اینجانب به‌مدت هفت‌سال، مدیر دوره دبیرستان پروفسور «مریم میرزاخانی» و دکتر «رویا بهشتی» بوده‌ام و نیز به‌مدت ۳۴سال، مدیریت مجتمع آموزشی «موسسه منظومه خرد» را بر عهده داشتم، مایلم چندعامل مهم در موفقیت این دوعضو برجسته جامعه‌ علمی جهانی را با نسل جوان دانش‌آموزان در هرکجا دنیا که هستند، مطرح کنم.

«مریم» و «رویا» هر دو در عمل نشان ‌دادند که باور دارند معلم، یک راهنما و تسهیل‌کننده است و این خودشان هستند که باید یاد بگیرند. آنها به‌خوبی یاد گرفته بودند که چگونه یاد بگیرند و توانایی‌هایشان را باور داشتند. «مریم» و «رویا» به‌صورت یک‌تیم واقعی با هم کار می‌کردند. سینرژی حاصل از این کار تیمی بسیار بالا بود. علاوه بر هوش سرشار و پشتکار، تواضع ویژگی ممتاز «مریم» و اعتمادبه‌نفس بالا، ویژگی ممتاز رویا بود. کار تیمی این دونفر باعث می‌شد که ویژگی‌های ممتازشان آنان را به‌پیش ببرد.

«مریم» و «رویا» هرگاه که اراده می‌کردند کاری را انجام دهند، با پشتکار بالایی در آن کار موفق می‌شدند. آنها همواره از امکاناتی که در اختیار همه دوستانشان هم بود، به‌خوبی استفاده می‌کردند. در موقعیت‌های فرامدرسه‌ای، مانند دانشجو رفتار می‌کردند، نه یک‌شاگرد مدرسه. هوش بالا، پشتکار، تواضع، اعتمادبه‌نفس، استفاده بهینه از امکانات موجود و کار تیمی از عوامل اساسی موفقیتشان بود. "

رویا بهشتی در ماه می 2003 دکترایش را از دانشگاه ام آی تی (MIT) زیر نظر پروفسور یوهان یانگ¹ دریافت نمود. او در حال حاضر دانشیار² ریاضی در دانشگاه واشنگتن در سنت لوئیس³ می باشد. حوزه تحقیقاتش، هندسه جبری⁴ می باشد. تحقیق او توسط بنیاد ملی علوم⁵(NSF) حمایت شده است. (DMS1204567)

هندسه جبری شاخه‌ای از ریاضیات است که مفاهیم جبر مجرد، به ویژه جبر جابجایی، را با مسائل هندسه می‌آمیزد. این شاخه از ریاضیات مدرن با آنالیز مختلط، توپولوژی و نظریه اعداد در ارتباط تنگاتنگ است. واریته مستوی (آفین) n-بعدی که یکی از بنیادی ترین مفاهیم این شاخه از ریاضی است دقیقا صفرهای مشترک تعدادی دلخواه از چند جمله ای های n-متغیره روی میدان مفروض تعریف می شود. بنابراین حلقه ی چند جمله ای ها نقش عمده ای در هندسه جبری ایفا می کند. تاریخ این علم گسترش فروانی دارد، طوری که قسمتی از مطالعات ارشمیدس مسائلی پیرامون مقاطع مخروطی، تشکیل می داد. همچنین ابن هیثم، فیزیکدان ایرانی قرن ۱۰ میلادی برای محاسبه ی مسافت ها مجبور به استفاده از معادلات درجه ی سوم می شده است. و نهایت اینکه خیام معادله ی درجه ی سوم را در کلی ترین حالت حل نمود. وی این کار را از طریق مقاطع مخروطی، و قطع دادن دایره با سهمی درجه دوم، انجام داد.

دیوید مامفورد⁶، پرفسور بازنشسته ریاضیات کاربردی در دانشگاه «براون» هندسه جبری را چنین توصیف می کند:

"هندسه جبری این شهرت را دارد که رشته ایست پیچیده، محرمانه و بسیار مجرد که طرفدارانش به طور سری در حال نقشه ریزی برای تصرف بقیه ریاضیات هستند و به نوعی این نکته آخر، درست است!"

تحصیلات:

1999: فارغ التحصیل دانشگاه صنعتی شریف (22 سالگی)

2003: دریافت دکترا از دانشگاه MIT آمریکا. (26 سالگی)

2003: پژوهشگر ارشد ریاضی، موسسه ریاضیات ماکس پلانک، آلمان (26 سالگی)

2004: فوق دکترا، عضو ارشد پژوهشی دانشگاه کویین، کینگستون کانادا (27 سالگی)

2006: فوق دکترای ریاضی عضو ارشد پژوهشی دانشگاه کالیفرنیا، برکلی آمریکا (29 سالگی)

2006: استادیار ریاضی دانشگاه واشنگتن در سنت لوئیس آمریکا (29 ساگی)

2009: دانشیار ریاضی دانشگاه واشنگتن در سنت لوئیس آمریکا (32 ساگی)

اولین تألیف رسمی:

رویا بهشتی به همراه دوست صمیمی اش، مریم میرزاخانی، کتابی جهت آمادگی برای المپیاد ریاضی با عنوان نظریه اعداد، تألیف و منتشر نمودند. جزئیات بیشتری از این کتاب:

$کتاب نظریه اعداد، تألیف رویا بهشتی و مریم میرزاخانی$

نام کتاب: نظریهٔ اعداد، از مجموعه کتابهای آمادگی برای المپیاد ریاضی

عنوان لاتین: Elementary Number Theory, Challenging Problems
تألیف: رؤیا بهشتی زواره، مریم میرزاخانی
ویرایش: ارشک حمیدی
چاپ هشتم - ۱۳۹۱
تعداد صفحات: ۳۰۴
شابک سیزده رقمی: ۹۷۸-۹۶۴-۳۱۸-۲۸۷-۸
شابک ده رقمی: ۹۶۴-۳۱۸-۲۸۷-۸
قطع کتاب: وزیری
وزن کتاب: ۴۲۴ گرم

پیشگفتار کتاب نظریهٔ اعداد
نظریهٔ مقدماتی اعداد چه از نظر مطلب و چه از نظر تنوع مسأله‌های مربوط به آن از زیباترین بخشهای ریاضیات مقدماتی است، و ویژگی بارز آن وجود مسأله‌هایی است که گرچه بیانی ساده و مقدماتی دارند، اما یا حل‌نشده باقی مانده‌اند و یا حل آنها نیاز به استفاده از ریاضیات پیشرفته دارد. در این کتاب به آموزش این بخش جذاب از ریاضیات مقدماتی پرداخته‌ایم، به‌گونه‌ای که برای دانش‌آموزان علاقه‌مند دوره‌ٔ دبیرستان مفید و قابل استفاده باشد. البته آنچه در این کتاب آمده بیشتر از آن مطالبی است که به زعم مؤلفان، دانش‌آموزان علاقه‌مند به شرکت در المپیادهای ریاضی باید بدانند، و برای این دسته از دانش‌آموزان مطالعهٔ فصلهای 1 تا 6 و فصلهای 14 تا 20 کافی است. برای مطالعهٔ این کتاب پیشنیاز خاصی بجز آشنایی با ابزارهای اساسی ریاضیات مقدماتی مانند اصل استقرای ریاضی و اصل لانه‌کبوتری لازم نیست.

فصلهای 1 تا 6 اساس فصلهای دیگرند، و برای مطالعهٔ بقیهٔ فصلها خواننده باید به مطالب آنها مسلط باشد. بهتر است فصلهای 7 تا 12 را دنبال هم خواند. در فصل 11 قانون تقابل درجهٔ دوم را بیان و ثابت کرده‌ایم. این قانون از مهمترین قضیه‌های نظریهٔ اعداد است و منشأ پیشرفتهای بسیاری در نظریهٔ اعداد بوده است. فصلهای 14 تا 21 همگی به بررسی جوابهای معادلات دیوفانتی اختصاص دارند. در این فصلها گاه از مطالب فصلهای 7 تا 13 استفاده کرده‌ایم؛ خواننده‌ای که این مطالب را نخوانده است، می‌تواند از مطالعه‌ٔ برهان قضیه‌ها یا راه‌حل مسأله‌های مربوط صرفنظر کند. هدفمان از آوردن فصلهای 25 و 26 آشنا کردن خواننده با برخی شباهتها میان ویژگیهای اعداد صحیح و ویژگیهای چند جمله‌ایهایی است که ضرایبشان اعدادی گویا هستند. هر چند این فصلها در انتهای کتاب آمده‌اند، اما می‌توان آنها را بعد از مطالعهٔ فصلهای 1 تا 6 خواند. در این کتاب تعداد زیادی مسأله آمده است. برخی از این مسأله‌ها را کامل حل کرده‌ایم. مسأله‌هایی که به‌عنوان تمرین در انتهای فصلها آمده‌اند، اغلب ساده‌اند و برای تسلط یافتن بر مطالب هر فصل حل کردن آنها مفید است. مسأله‌هایی که به‌عنوان تمرینهای تکمیلی آمده‌اند، دشوارترند، و بعضاً از میان مسأله‌هایی انتخاب شده‌اند که در المپیادهای مختلف مطرح یا پیشنهاد شده‌اند.

آقای دکتر یحیی تابش مشوق ما در نگارش این کتاب بوده‌اند. از ایشان برای راهنماییها و نظرات مفیدشان تشکر می‌کنیم. همچنین از آقای ارشک حمیدی، ویراستار کتاب، برای پیشنهادات ارزشمند و زحمات فراوانشان در ویرایش این کتاب سپاسگزاریم.

رؤیا بهشتی زواره - مریم میرزاخانی -- شهریور 78

برای اطلاع از سایر مقالات و تألیفات دکتر رویا بهشتی، اینجا کلیک نمایید: لیست مقالات دکتر رویا بهشتی

منبع: زندگینامه ریاضیدانان: رویا بهشتی زواره

:: اختصاصی گروه تدوین محتوای آی هوش

استفاده از این مطلب و انتشار آن، با ذکر نام آی هوش و درج لینک www.ihoosh.ir، بلا مانع است.

اختصاصی آی هوش رویا بهشتی زواره

آی هوش جمعه 31 مرداد 1393 ساعت 16:09

0 نظر

تکنیک بارش مغزی: مریم میرزاخانی رموزش را آشکار می کند

عکس از: Quanta Magazine/ مریم میرزاخانی

مریم میرزاخانی، ریاضیدان ایرانی الاصل، استاد دانشگاه استنفورد، اولین زنی که موفق به کسب مدال فیلدز در ریاضیات شده است. این مدال بالاترین رتبه در این رشته و برابر با جایزه نوبل است که هر چهار سال یک بار به یکی از ریاضیدانان برجسته جهان اهدا می شود. میرزاخانی این جایزه را به سبب تلاش هایش در زمینه هندسه پیشرفته و جا به جایی های فضایی به دست آورده است. میرزاخانی اعلام کرده که پس از دریافت این جایزه مایل به گفتگو با رسانه ها نیست اما گفتگوی مفصلی که قبل از کسب این جایزه با مجله کوانتا داشته، نشان می دهد که او از چه تکنیک هایی برای پرورش ذهن و به خصوص بارش مغزی استفاده می کند.

آهسته و پیوسته حرکت کن

مریم میرزاخانی با فروتنی اعلام می کند که ذهن کندی دارد بنابراین اجازه می دهد مسائل ریاضی، به آرامی و در طولانی مدت در ذهنش جای بگیرند. او برای آموختن عجله نمی کند و اجازه می دهد ذهنش با سرعت آرام ولی به طور پیوسته ای، با مسائل رو به رو شود. میرزاخانی دوست دارد خودش را کند بداند. بر خلاف بسیاری از ریاضیدانانی که محاسبات ذهنی را با سرعت فوق العاده ای انجام می دهند، او اعلام می کند که برای درک و حل مسائل گاه چند سال وقت صرف می کند. او می گوید: "ماه ها یا حتی سالها بعد می توانی وجوه دیگری از مسائل را ببینی که در آغاز کار از چشمت پنهان بوده اند. مسائلی هست که نزدیک به یک دهه ذهن من را به خود مشغول داشته اند و هنوز پاسخ قطعی برای آنها نیافته ام."

این تکنیک بارش مغزی بلند مدت، تنها مختص به میرزاخانی نیست بسیاری از دانشمندان و مخترعان، سالها وقت صرف تفکر به راه حل مسائلی که ذهنشان را درگیر کرده نموده اند. بنابراین بارش مغزی در این افراد نه ناشی از حرکت تصادفی اطلاعات در ذهن بلکه ناشی از یک بستر آگاهی فزاینده و هشیار است. روان شناس مشهور، میهالی چیک سنت میهالی¹ در این باره می گوید "محاسبات شناختی گاه از طریق یک روند طولانی جایگزینی های ذهنی روی می دهد ذهن انسان گاه به طور ناهشیار و حتی در خواب، در حال تفکر و پیدا کردن پاسخ به سوالات ما است."

افکارت را روی کاغذ بیاور

میرزاخانی افکار خودش را روی صفحات کاغذی بزرگ طراحی می کند. او می گوید "کشیدن ایده ها به شما کمک می کند که با موضوع ارتباط بهتری برقرار کنید و زوایای جدیدی از آن را ببینید لازم نیست تمام جزئیات را بنویسید تنها نکات اصلی را بنویسید و ارتباط بین افکار خود را طراحی کنید." تحقیقات بسیاری نیز بر نقش به روی کاغذ آوردن افکار و ایده ها در حل مسائل تاکید می کنند. یکی از کارشناسانی که روی این موضوع تحقیق کرده، سانی براون²، در این باره می گوید " به روی کاغذ آوردن ذهن شما را انسجام و نظم می بخشد"

کار میرزاخانی با کسب جایزه به پایان نرسیده و او دوباره به میدان تحقیق باز می گردد با این امید که این جایزه به زنان دیگر نیز در این حوزه امید و انگیزه ببخشد. "این افتخار بزرگی است اگر الهام بخش دانشمندان و ریاضیدانان زن باشد. اطمینان دارم در سالهای آینده زنان بسیار بیشتری، چنین جایزه ای را کسب خواهند کرد."

پی نوشت:

1. Mihaly Csikszentmihalyi

2. Sunni Brown

منبع: تکنیک بارش مغزی: مریم میرزاخانی رموزش را آشکار می کند.

:: اختصاصی گروه تدوین محتوای آی هوش

استفاده از این مطلب و انتشار آن، با ذکر نام آی هوش و درج لینک www.ihoosh.ir، بلا مانع است.

:: در این رابطه بخوانید:

-- نور چشم ایرانیان، افتخار جامعه جهانی ریاضی نوشته دکتر زهرا گویا - استاد دانشگاه شهید بهشتی

-- ساده و بی تکلف، پرتره ای از مریم میرزاخانی چهره ی ساده و بی تکلف از یک ریاضیدان نابغه

-- کار بزرگی که میرزاخانی کرد از زبان مهدی بهزاد - چهره ماندگار ریاضی ایران

-- تبریک رییس‌جمهور به خانم پروفسور مریم میرزاخانی

-- المپیادی عاشق «هذلولی» و «خط خطی» چگونه تاریخ‌ساز شد؟